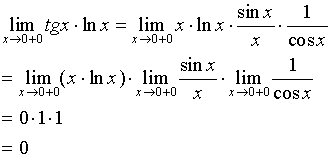§3.2
罗必达法则
当![]() ( 或
( 或![]() )时,两个函数
)时,两个函数![]() 与
与![]() 都趋向于零或都趋向于无穷大,那么,极限
都趋向于零或都趋向于无穷大,那么,极限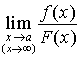 可能存在,也可能不存在。通常把这种极限叫做不定式,并分别简记为
可能存在,也可能不存在。通常把这种极限叫做不定式,并分别简记为![]() 型或
型或![]() 型。
型。
对不定式,不能简单地用“商的极限等于极限商”这一求极限法则来处理。求不定式极限有一种简便方法
—— 罗必达法则,见下述两个重要定理。
一、基本类型的不定式
![]() 型
型
【定理一】设
(1)、当 ![]() 时,函数
时,函数![]() 及
及![]() 都趋于零;
都趋于零;
(2)、![]() 及
及![]() 在点
在点![]() 的某个邻域内(点
的某个邻域内(点![]() 本身除处)存在,且
本身除处)存在,且
![]() ;
;
(3)、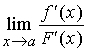 存在(或无穷大),
存在(或无穷大),
则 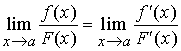 。
。
【证明】因为求极限
 与函数值
与函数值 ![]() 、
、![]() 无关,
无关,
那么我们可设:![]() , 这并不会影响极限
, 这并不会影响极限 。
。
由这一假设及条件(1)、(2)两款知:
![]() 与
与![]() 在点
在点 ![]() 的某个邻域内是连续的, 设
的某个邻域内是连续的, 设![]() 是这邻域内的一点,
是这邻域内的一点,
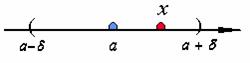
那么在以![]() 及
及![]() 为端点的区间上,
为端点的区间上, ![]() 与
与![]() 全部地满足柯西中值定理的条件,因此有
全部地满足柯西中值定理的条件,因此有
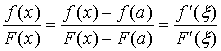
当![]() 时,
时, ![]() ,而由(3)款知
,而由(3)款知 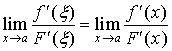
故 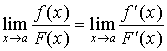 。
。
为了更好地使用这一定理求极限,给出几点重要注解:
1、此定理用来处理![]() 时的
时的![]() 型不定式极限问题。这种通过分子与分母导数之比的极限来确定不定式极限的方法称之为罗必达法则。
型不定式极限问题。这种通过分子与分母导数之比的极限来确定不定式极限的方法称之为罗必达法则。
2、如果极限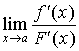 仍属于
仍属于![]() 型, 且
型, 且![]() 、
、![]() 又满足定理中的条件,则可以再使用罗必达法则。即
又满足定理中的条件,则可以再使用罗必达法则。即
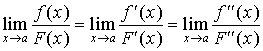
3、如果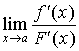 不存在,不能断言
不存在,不能断言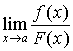 也不存在,只能说明该极限不适合用罗必达法则来求。
也不存在,只能说明该极限不适合用罗必达法则来求。
反例:极限  存在,
存在,
而使用罗必达法则 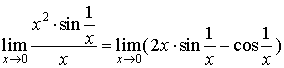 不存在。
不存在。
【例1】求极限
(1)、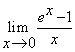 (2)、
(2)、![]()
【解】
![]()
上述定理仅是适合于![]() 时的
时的![]() 型不定式;对于
型不定式;对于![]() 时的
时的![]() 型不定式,我们也有相应定理。
型不定式,我们也有相应定理。
【定理二】设
(1)、当![]() 时,函数
时,函数![]() 及
及![]() 都趋向于零;
都趋向于零;
(2)、![]() 及
及![]() 当
当![]() 时存在,且
时存在,且![]() ,
,![]() 是充分大的正数;
是充分大的正数;
(3)、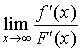 存在 ( 或无穷大 )
存在 ( 或无穷大 )
则 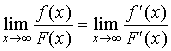 。
。
这一定理的证明略。定理一的注解对它同样适用,仅需将![]() 改成
改成![]() 即可。
即可。
【例2】求极限
(1)、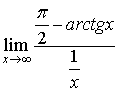 (2)、
(2)、

【解】
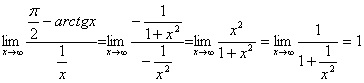
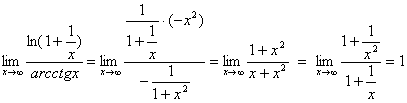
对于![]() (或
(或 ![]() )时的
)时的 ![]() 型不定式,我们有如下相应的定理; 定理一的注解以它们仍适用,仅需作相应地改动。
型不定式,我们有如下相应的定理; 定理一的注解以它们仍适用,仅需作相应地改动。
【定理三】设
(1)、当![]() 时, 函数
时, 函数![]() 及
及![]() 都趋向于无穷大;
都趋向于无穷大;
(2)、![]() 及
及![]() 在
在![]() 点的某个邻域内(
点的某个邻域内(![]() 点本身除外)存在,且
点本身除外)存在,且
![]() ;
;
(3)、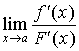 存在 (或无穷大),
存在 (或无穷大),
则 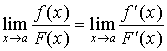 。
。
【定理四】设
(1)、 当![]() 时, 函数
时, 函数![]() 及
及![]() 都趋向于无穷大;
都趋向于无穷大;
(2)、 ![]() 及
及![]() 在
在![]() 时存在,且
时存在,且![]() ,
,![]() 是充分大的正数;
是充分大的正数;
(3)、 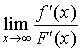 存在 ( 或无穷大 ),
存在 ( 或无穷大 ),
则 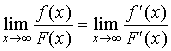 。
。
【例3】求极限
(1)、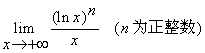
(2)、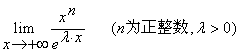
【解】
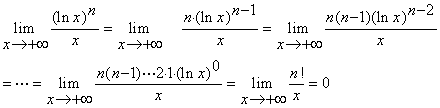
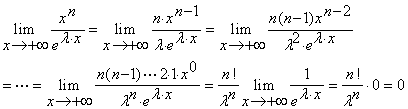
此例中的正整数![]() 改为一般正实数
改为一般正实数![]() 时,结论仍成立。 同学们可以自行验证。这样,我们获得了一把函数趋向于无穷大的快慢标尺。
时,结论仍成立。 同学们可以自行验证。这样,我们获得了一把函数趋向于无穷大的快慢标尺。

二、其它类型的不定式
上述类型的不定式均可化归为 ![]() 型或
型或![]() 型的不定式。
型的不定式。
【例4】 ![]()
【解】
![]()

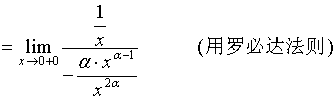
![]()
结论可推广到一般 ![]()
【例5】 求![]()
【解】

![]() 型的不定式,一般是幂指函数的极限,可采用对数求极限法。
型的不定式,一般是幂指函数的极限,可采用对数求极限法。
【例6】 求 ![]()
【解】
设 ![]()
取对数 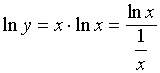
对对数函数![]() 求极限,最后转化为对函数
求极限,最后转化为对函数![]() 的极限。
的极限。
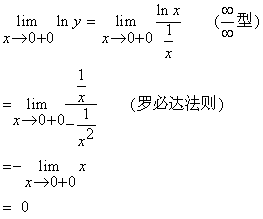
从而有 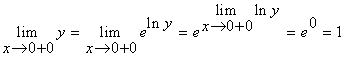
【例7】 求 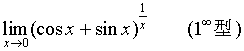
【解】
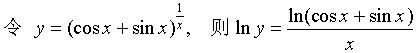

故 ![]()
【例8】求
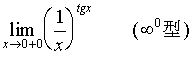
【解】
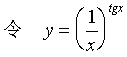
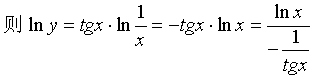

![]()
三、求极限的一个重要工具包

利用这几个工具极限、求极限四则运算法则,可帮助我们快速地求出许多较为复杂的极限。
【例9】求极限 ![]()
【解】已知极限
![]()